

Now you have seen my previous antenna pages containing basic information about Antennas and Baluns, all that remains is to add some info about feeders. With this you will have the whole picture, from antenna to receiver/transmitter. I will briefly mention waveguides, but I will not give any information since their use is a bit specialised.

A feeder is simply a method of conveying the RF energy between an antenna and a receiver or transmitter. Without the feeder cable, the only efficient place to operate your transmitter will bu up a tree or your radio mast. The object of the feeder is to transport as much power as possible with as little loss as possible. From now onwards I will only consider an antenna and a transmitter; I will conveniently forget about receiving for the moment.
Feeders come in many forms, such as:
Open Line feeders are probably the most efficient feeders for HF work and comprise two wires separated by an insulator at convenient intervals. This type of feeder is ballanced, that is to say, that each conductor carries an equal and opposite current. They work on the principle the signal radiated by each wire is 100% cancelled out by the other.
Waveguides can be likened to a many resonant cavities with open ends, placed end-to-end. The physical size of the cavity is directly related to a wavelength, so waveguides at frequencies below about 2GHz are either impractical or very large (and expensive).
Coaxial cable is the most common form of feeder used in amateur radio work since the losses are acceptable for HF/VHF and the price (frequently) falls within a working manīs pocket. Radio energy contained inside the outer metal tube which acts as an Earth or screen to contain the signal. The RF power is assumed to be conducted down the centre conductor. This type of feeder is unballanced, as are the outputs from most radio transmitters and receivers.

A feeder can be thought of as composed of a series of inductors, each with a capacitance between the conductors. That is the way you could think of it, but in reality is is just one looooong inductor with a continuous capacitance to the other conductor. But let us stick to the concept of loads of individual LCs.
If you were to apply a logic voltage "step" to the end of the feeder then each inductor will oppose the change. The following capacitor will take time to charge up. Thankfully, this charging time is VERY fast, when compared to the much longer rise-time of an RF waveform. In reality it would be typically many thousands of times faster, but it is still there. The result of this is that if you connected that logic level "step" to the cable and watched the step at the other end, then you will observe two effects:
In other words, the feeder cable imposes a time delay and has an attenuation that is related to frequency. If the capacitance C in the above representation were very low, then the signal could travel at typically a little less than 300,000,000 metres per second. This is about the speed of light, so the "delay rate" or "VELOCITY FACTOR" would be 1. But if the feeder had another material between the conductors other than air, then C would rise, depending upon the dialectric constant of the material. This would increase the "delay rate" or reduce the "VELOCITY FACTOR". If you know the dielectric constant (K) if the insulating material then the VF=1/(Sqrt(K)).
A typical VF for cheap 1/4" coaxial cable (URM76 or RG58) is 0.66 so that a radio wave will only travel at 200,000,000 metres per second (300,000,000 x 0.66 = 200,000,000). 0.66 is also a typical VF for mosr coaxial cables. A typical VF for Open Line feeder would be 1.

Real-live feeders have resistive losses, so the thicker the conductors, then the smaller are the losses. If, however the inductance and capcitance per unit metre can be reduced, then so can the losses. Cable manufacturers usually give the loss of a cable type as the number of Decibels per unit length, usually 10 metres. Microwave (Satelite TV cables) often quote a loss for 100 metres length. Here are a few examples of coaxial cable losses:
| Coax Type |
Impedance Z |
Losses (dB) per 10m length (-) = no information | Capac. (pf/metre) |
||||
|---|---|---|---|---|---|---|---|
| 10MHz | 100MHz | 200MHz | 400MHz | 1000MHz | |||
| URM43 | 50 | - | 1.3dB | - | - | 4.46dB | 100 |
| URM67 | 50 | - | 0.68dB | - | - | 2.52dB | 100 |
| URM70 | 75 | - | 1.5dB | - | - | 5.2dB | 67 |
| URM76 | 50 | - | 1.6dB | - | - | 5.3dB | 100 |
| URM95 | 50 | 0.86dB | 2.7dB | - | - | 10.2dB | 100 |
| RG58 | 50 | 2dB | - | 3.1dB | - | 7.6dB | 100 |
| RG59 | 75 | 0.37dB | 1.2dB | - | - | - | 51 |
| RG174 | 50 | 1.1dB | - | 4.2dB | 6dB | - | 100 |
| RG178 | 50 | 1.8dB | 4.4dB | - | - | 14dB | 96 |
| RG179 | 75 | 1.9dB | 3.2dB | - | - | 8.2dB | 100 |
| RG213 | 50 | 0.18dB | 0.62dB | - | - | 2.63dB | 100 |
| RG214 | 50 | 0.22dB | 0.76dB | - | - | 2.9dB | 96 |
| RG223 | 50 | 0.39dB | - | 1.58dB | 5.41dB | - | 96 |
| RG316 | 50 | - | 36dB | - | - | 190dB | 102 |
| URM203 | 75 | - | 0.75dB | - | - | 2.9dB | 56 |
| URM203a | 75 | - | 0.8dB | - | - | 3.0dB | 56 |
| CT100 | 75 | - | 0.49dB | 0.71dB | 1.2dB | 1.67dB | ?? |
You will notice that some manufacturers quote different frequencies. This should depend upon the intended use of the cable, but it varies almost as much as ASCII (American Standard Code for Information Interchange) varies from one computer to another.

There are a lot of misconceptions about the impedance of a coaxial cable. It is the inductance and capacitance per metre that determines the characteristic impedance of a coaxial cable, but the impedance of the cable is totally independant of the length as long as it is correctly terminated. This means that if you were sending 150MHz down a 50-ohm cable of infinite length, then the cable would indeed have a 50-ohm terminal impedance. If you cut the cable to ANY other length and terminated it with a 50-ohm resistor, then the impedance at the transmitting end would remain 50-ohms. As long as the end load is a resistive load that absorbs all the power presented to it, then the impedance at any point in the cable will remain a constant along itīs length.
I know that this fact is very unpopular and many people have tried to correct me via e-mail. 50-ohm cable is in reality still 50-ohm cable, thatīs how it got itīs name. The examples and proofs presented to me by mail all have one thing in common - mismatch. Here is one technical question I recently received:
Hi Harry,
I know that voltage and current in a coaxial cable vary and
so does the impedance. How can I calculate how much coax to use to match a
75-ohm dipole antenna with a 1:1 balun? You last wrote that the impedance
never varies in a perfectly matched coaxial feeder, if that is so then
how is it you CAN choose a feeder length to match a different impedance?
Take that last statement "... to match a different impedance ..." which really means that there IS a mismatch - the feeder is therefore NOT perfectly matched.
Read the next paragraph:

If our feeder is perfectly matched, then the impedance along itīs length IS a constant. Let us stuff a 100MHz 50-watt transmitter into the infinite length feeder. The transmitter is 50-ohms output, the feeder is 50-ohms, so the each cycle will run down the feeder, away from the transmitter at the speed of light (ignoring VF). If you were to take out your sine-wave surf-board and ride the wave, you too would travel at the speed of light, with only the sun in your face. Ok, it wold be a bit windy, but forget about that.
Now, let us cut the feeder and put a 50-ohm resistor on the end of the coaxial cable. Now you can still ride the wave on your sine-wave surf-board with only the sun in your face, but the wave would suddenly stop when it was all burned up in the resistor. If you were to monitor the current and voltage at any point in the coaxial cable then both would be a constant since the wave is still travelling and without impediment.
Now let us change the 50-ohm resistor for a 25-ohm resistor. The transmission line is no-longer matched. The 25-ohm resistor would no-longer burn 50 watts, but would have only 1/2 the voltage across it. Since power cannot be destroyed and cannot be 100% burned up, there is only one way for it to go - back down the line where it came from. If you were now to ride the forward wave with your sine-wave surf-board then you would meet more waves coming at you at the speed of light. Since you are also travelling at the speed of light, the reflected wave would be hitting you at twice the speed of light.
A stationary observer would see you being hit every 1/2 wavelength, and if the observer could see the waves, then he would see the waves adding and subtracting at 1/2-wave intervals. He would see 50-volts RMS moving away from the transmitter and 25-volts leaving the resistor towards the transmitter. He would see a pattern where the forward 50v would have 25v added (75v peaks) and he would also see 50v being partially cancelled by 25v (25v troughs). The ratio of 75v to 25v is 3:1 and is known as the Voltage Standing Wave Ratio (VSWR). Since the mismatch (the 25-ohm resistor) is stationary, then the forward and reflected additions and subtractions would always be stationary and occur at the same place in the coaxial cable.
Although I have over-simplified this a little, I hope that some form of clarification will be given to those who find it hard to understand. But let us delve a little deeper into our now mismatched coaxial transmission line. What has happened to the impedance?
These additions and subrtactions of our transmission line will also affect the impedance since the current and voltage are now dependant upon the location in the transmission line. 1/2-wavelength back from the 25-ohm resistor, if we were to measure the impedance then it too would be 25-ohms. In fact, the impedance would be 25-ohms 1/2-wavelength and every 1/2-wavelength thereafter. Between these 25-ohm impedance points there would be a higher impedance - 100-ohms.

Not without correcting the impedance mismatch. We can place an "Antenna System Tuning Unit" (TU, ATU, AMU, ASTU or ASTCU) between the coaxial cable and the 25-ohm resistor. This would just be an impedance transformer to convert 50-ohms down to 25-ohms. A 2:1 balun would do exactly the same job. If the 25-ohms terminating were an antenna at the top of a tree then you may have a problem. An ATU up the tree would be a bit of a bugger to tune and would have to be waterproofed. If the mismatch were to vary with frequency, then you would be up and down that ladder every time you operated.
It is common practice to place the ATU between the transmitter and the coaxial cable. In this event, it does NOT cure the problem, but makes it look as if the problem has been cured. It creates another bad VSWR so that the reflected power is re-reflected back towards the mismatch. A load of that re-reflected power will be absorbed by the load, but the even smaller portion that is re-re-reflected will go back to the ATU yet-again. In this way, it will keep bouncing back and forth until eventually it will all be absorbed by the mismatched load.
Now you can probably understand that the instantaneous power in a mismatched transmission line is somewhat higher than in a matched line. It is for this reason that it is often under a (corrected?) mismatch that baluns and antenna/feeder insulators most often fail, and occasionally with quite spectacular visual effects. You will also realise that RF power is bouncing back and forth through the same feeder losses, time and time again. The feeder will therefore dissipate more power, and less power will be dissipated by the load.
It is my personal opinion that a transmisson line should ALWAYS be matched. An ATU itself is a passive device and therefore has a signal loss. It is far better to have a resistive antenna that is corectly matched tot he feeder. Having said that, there are occasions where a mismatched transmission line can be used.

Yes! If you had an antenna that was the wrong length, then you can add a bit of feeder to it to make it the right length. The remainder of the feeder would then have to be an EXACT multiple of 1/2-wavelengths to reach the transmitter.
This technique is knows as "Resonant Feeder". All resonant feeder systems therefore begin at the load as a mismatch. In this way one can make an antenna appear (at the transmitter) to resonate at more than one frequency that are NOT harmonically related, eg 7MHz and 10.1MHz. The most well known such antenna is the G5RV antenna.

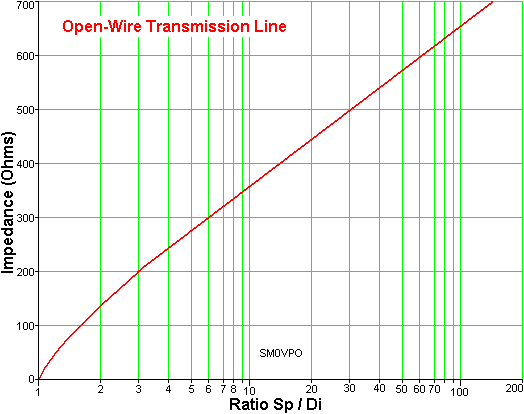
The stuff is very easy to construct, as far less loss than coaxial cable and (this is the part I like) it is cheaper. The only factors that affect the characteristic impedance of an open-wire feeder system is the diameter of the wires used and the distance between them. The formula is:
Z = 276 x Log(2 x Sp / Di)
Where:
The spacers that hold the two wires apart can be anything that insulates; plastic pipes, rings, book-binders, polythene, even a 1/4-wave aluminium stub will work for a single frequency! Take a trip to your local Ikea. The nylon kitchen chopping boards are great for bringing feeders into the shack. The office section is full of thin plastic things that can be used as spacers.
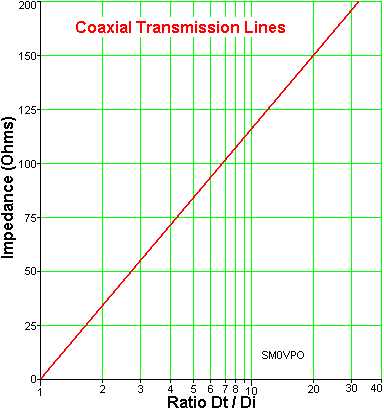
This stuff is not very easy to construct, but in essence it is just a conductor inside a tube. If you are making VSWR bridges or any "through line" RF meter then you will need to make a bit of coaxial transmission line. The only factors that affect impedance are, the Inside-Diameter of the outer conductive surface, and the outside diameter of the conductor. The formula is:
Z = 138 / (Log(Dt / Di))
Where:

Well, that is about all I intend to write about feeders. If anyone can help me fill in the feeder data table then I am always ready to receive new data. I am also looking for the data for Andrews LDF250 and LDF450 cables. Best regards from Harry - SM0VPO (Märsta).
Return to INFO page