

This has become a sort of regular periodic question - "Harry can you please explain how the FM Wireless microphone functions?", "... and can you include the calculations?". Ok, this I can do, and I shall try to give clickable calculations whenever possible. Of course, this page is not for the experienced constructor, but I am please that so many people seem to take an interest in my homepages and the techniques I use. So I shall start with a simple one-transistor device and build up the circuit.
Some of the formulas given are just rough, in the interest of simplicity.
Nearly all my circuits are drawn with a positive and negative supply rail connected to a supply, of some description. Small voltage across a transistor cause the internal CB capacitance to rise, in effect it is a small varicap diode. Another consideration is the box - many commercially available hobby boxes (enclosures) have an integral 9v PP3 type battery compartment. So I will use a 9v battery for this project (calculate a little lower than 9v).

The basic circuit is an emitter follower transistor amplifier. This gives us a current amplification, but no voltage amplification. In the interest of stability I will run the transistor base at 50% of the supply voltage. Small voltage changes will therefore NOT affect the transistor capacitance changes by much. I will also run the transistor at about 10mA (0.01A). The BC547 is rated at 300mA, so 3% of this is a nice general figure. The transistor will not get hot, but there is enough current to allow it to work, but not enough to flatten a battery in a couple of hours.
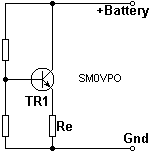
The emitter resistor Re is therefore selected to give an emitter current of 10mA (0.01A). The emitter voltage is equal to the base voltage (Vbatt = 9v / 2 = 4.5v), minus 0.7v = 3.8v. Re is therefore equal to E / I = 3.8 / 0.01 = 380 Ohms. I select the next lowest common value of 330 Ohms because the battery will have a tendency to fall, not rise. If you want an on-line formula then here it is. Enter the battery supply voltage (Vbatt) and your chosen transistor standing emitter current (Ie). You can use this formula to re-calculate the component values for other supply voltages.
Formula for calculating emitter resistor:
| Resistance Re | = | (Vbatt -0.7) / Ie |
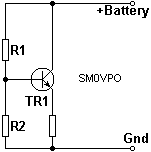
The supply divider resistors feeding the base of the transistor are of equal value, so that the transistor base is fed with half the supply voltage. You can use other values, such as to set the base to only a quarter, but the complete transmitter will be more sensitive to supply voltage changes, and the modulation sensitivity will also be more variable.
The BC547B transistor current gain (hfe) is about 300, according to the specifications, but I find that it is typically 350 or more. But we will base our calculations on 200, mainly because people will try to use other transistors without changing the values.
R1 and R2 must therefore divide the battery voltage by two, without the voltage falling much due to the transistor base current. The transistor base current is equal to the emitter current divided by the transistor current gain (hfe).
Formula for calculating TR1 base current:
| Current Ib | = | Ie / hfe |
In our case it is about 25uA (0.000025A). R1 and R2 must therefore burn at least 4-times this figure. In more critical circuits use a higher value, such as 10 times, but I think a lot about battery drain so I choose 4x.
| Resistance R R1 + R2 |
= = = = = |
E / I Vbatt / Ib 9 / 4Ib 9v / 100uA 90K Ohms |
R1 and R2 must therefore each be half this value = 45K. Nearest preferred value = 47K. Ok, time for another formula. I have already entered the results of the previous calculator, but change them manually if you want.

The next task is to add capacitors to the DC project. The first set of capacitors are the radio capacitors, of which there are two. One capacitor controls the frequency, and the other controls the level of feedback. I we will begin with frequency (C1), and also workout the inductor, since this component is also related to frequency. The transistor will be used as a "Common Base" amplifier circuit for the oscillator part. This means that the input is the emitter, and the output is the collector.
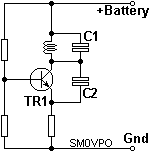
The RF impedance at the collector in this application is related to the output power level in a very minor way: the impedance is more related to VHF capacitive effects and outside influences. An oscillator of this type will normally have a collector impedance of 1/3 of the emitter impedance. Why? I will come to that in a moment. In this circuit, C1 will have an impedance of about 100 Ohms, which is half of the emitter resistor in my example. I also know that it will be operating at 105MHz, the top end of the FM broadcast band. Now we have enough data for a calculation. Formula:
Where Xc is in Ohms, Pi is 3.1415926535...(ish), F is frequency in Hertz, and C is capacitance in Farads. Transpose the formula to get the capacitance value:
| Capacitance |
= = = = |
1 / (2 * 3.142 * 1.05E8 * 1.0E2 1 / 1.018E11 0.000 000 000 015 155 648 510 199 Farads 15pf (approximately) |
In the real world there will be circuit capacitance, so I stick my wet finger in the wind, then subtract 2 - 3pf, or so to give a practical value of 12pf. But let me use a formula to stop you falling over all those zero's. I will also build in the decimal corrections so you can enter MHz, pf, and uH directly.
There is a slight discrepancy from my example figures since the calculator uses a much greater precision.
C2 is the feedback capacitor that starts the oscillations. This should be about 1/5 of the value of C1 and depends upon the maximum operating frequency (Ft) of the transistor. The BC547B can operate up to 300MHz. If the oscillator does not start, then you can increase the calue of C2. C2 value should be chosen for twice the value that allows oscillations to start. For the BC547B this is 1/6, or 2.5pf. This value is so small that circuit layout will have a dramatic effect on it, so precision is not needed. But if you have inserted values into the previous formula, then the value of C2 should be:

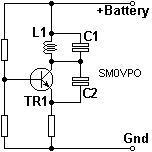
This one is easy. We know the value of C1 at 105MHz, and the reactance of the inductor and capacitor are equal at resonance. So we know we need a reactance of 100 Ohms at 105MHz. Basic inductive reactance formula is:
Where F is in Hertz, L is in Henries, and Pi is still approximately equal to 3.142
Transpose the formula for unknown inductance value and we have the formula we need:
| Inductance |
= = = = |
100 / (2 * 3.142 * 1.05E8) 100 / 6.5982E8 1.5155648E-7 0.15155uH |
Now we have the inductance, so how many turns of wire is that on a 6mm Dia. drill bit? The coil shall have no ferrites, or other metalic core. The suggested diameter is 6mm and the winding length is 10mm. Again, enter your own values if you want a different sized coil.

Ok, so now we have an oscillator that looks as though it should work. In reality it STILL may not work at all. The battery supply wires are big inductors, and the battery is resistive. This means that signals can be modulated on the supply voltage rail, and passed to other parts of the circuit. With multi-stage circuits this can be a major problem and cause instability, self-oscillation, harmonics, or even prevent the oscillator working at all. What we need to do is to make the battery supply a low impedance to both RF (100MHz region) and audio (100Hz region).
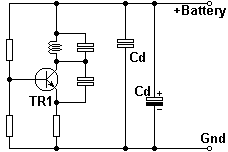
Real-world capacitors have both inductance and capacitance. This gives them resonance. It is therefore customary to have at least two supply decoupling capacitors of quite different values. This will usually be 1nf (1000pf) across every digital logic chip, and every low-power RF stage. For low-power HF work these will become 20nf or more. In addition to this there will be at least one large electrolytic capacitor on a small project like this. The value should be at least 0.47uf for low-level audio circuits. I used 220uf on mine.

If you have religiously built the above circuit then you are going to be dissapointed. It will not work. The oscillator uses a comon base configuration. This means signal out of collector, into emitter. The base must be at RF ground. It is not: it only has a pair of 47K resistors in parallel, giving it a 22K impedance to ground. We need another capacitor to make the oscillator work. Enter C3.
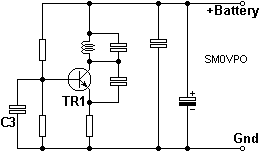
C3 connects the transistor base to ground, as far as RF is concerned. The problem here is that the base of the transistor is also our audio input. If we used a 1000uf capacitor here then it would oscillate (after a minute or so), but there would be no modulation. C3 must have a low impedance to RF, and a high impedance to AF.
C3 could be replaced with an RF quartz 3rd or 5th harmonic crystal, to make a crystal-controlled oscillator. If you did this then the oscillator would never take frequency modulation (FM). It would become "CW only".
It is considered to be a short-circuit to RF if the impedance is 1/10 of the impedance it shunts. We are effectively reflecting the emitter back to the base, but the hfe of the transistor is doing some of the job for us. The emitter load (Re) is 330 Ohms, the chosen hfe=200 for our worked examples. The formula for the required C3 impedance is
We then take the impedance and calculate the capacitance at the lowest operating frequency (88MHz), using the good-old transposed capacitive reactance formula:
In our example the reactance is:
| Reactance |
= = = |
(Re * hfe) / 10 (330 * 200) / 10 6600 Ohms (6.6E3) |
The capacitance needed here is therefore:
| Capacitance |
= = = = = |
1 / 2*Pi*F*Xc 1 / 2 * 3.142 * 8.8E7 * 6.6E3 1 / 3.6497E12 2.739915E-11 27pf |
Note that this is the MINIMUM capacitance needed. We can still increase the value a LOT because our FM oscillator can have a modulation frequency of up to 8.8MHz with C3 = 27pf. A decoupling capacitor is like cracking an egg. Whe have just calculated the smallest spoon needed, but there is nothing to stop us using a hammer, or even a dirty-great brick. Use a 270pf as a practical value, so the highest modulating frequency is just under 1MHz, and the oscillator is not working near the edge of it's operating point.
Ok, let us put C3 into a calculator for you. Again, I have put in the default values from the previous calculations, so you only need to add the lowest operating frequency and click the button. But you can of course choose to enter other values:

The last component is the AF input, C4. We need a capacitor to couple audio in, without disturbing the DC bias conditions. The input impedance of the base circuit is the emitter resistor multiplied by hfe. This is also in parallel with our two biasing resistors.
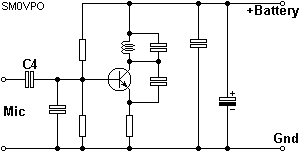
R1 and R2 are in parallel with each other, so the impedance here Zr = R1/2 (or R2/2).
| Zr |
= = = |
R1 / 2 47K / 2 23.5K |
As already stated, the base impedance Zb = Re * hfe.
| Zb |
= = = |
Re * hfe 330 * 200 66K |
The input impedance Zin = (Zr * Zb) / (Zr + Zb).
| Zin |
= = = = |
(Zr * Zb) / (Zr + Zb) (23.5 * 66) / (23.5 + 66) 1551 / 89.5 17.33K Ohms |
The input capacitor needs to have a reactance value of 1/5 of this at the lowest input audio frequency.
| Xcin |
= = = = |
Zb / 5 (23.5 * 66) / (23.5 + 66) 17.33K / 5 3.466k Ohms |
So what value of capacitor has a reactance of 3.466k Ohms at 100Hz (my chosen lowest audio frequency)? Use the simple capacitive reactance formula, transposed for unknown capacitance:
| Capacitance |
= = = = = |
1 / 2*Pi*F*Xc 1 / (2 * 3.142 * 1E2 * 3.466E3) 1 / 2.178E6 0.4591E-6 0.45uf (450nf) |

If you entered 8v (a practical 9v battery) and selected 10mA, then accepted all my suggestions, then you will have re-created the oscillator section of my V5 FM wireless microphone project. My inner thoughts and calculations are there, so is the method to easily change the values for other frequencies, even the coil winding data.

The complete circuit is here, with the values in the calculators. Remember that there is a lot of leeway, and in many cases a component value is really just an educated compromise. C4 can be reduced in value to add a measure of pre-emphasis.
The output circuit is a tapping on L1. Connect the antenna to the collector of TR1 and you will get about 10mW of power, but don't breathe. It is very unstable. Instead, take a 1% tapping from the top of L1 and it will be megga-stable, but have no output power to speak of.

I have used the decimal notation "E" to to express magnitude, so 3.0E0 = 3, 3E-6 = 0.000003, 3E99 = BIG, and 108MHz = 1.05E8MHz. This great for expressing large numbers - According to one book, there are only between 1E79 and 1E89 molecules in the universe. Interesting that one of these figures is ten-thousand-million times bigger than the other!
But this does mean that I can count down to 100pf (E-10) on my fingers, and down to 1pf by removing only one sock.
In the worked examples I have assumed the value of Pi to be 3.142, but in the calculators I have taken it to be 3.1415926535 (10 decimal places). In reality, 3 is close enough for most practical component calculations: within 5%. If you want to be bloody-minded, then here is Pi to 4000 decimal places :-)
3.141592653589793238462643383279502884197169399375 10582097494459230781640628620899862803482534211706 79821480865132823066470938446095505822317253594081 28481117450284102701938521105559644622948954930381 96442881097566593344612847564823378678316527120190 91456485669234603486104543266482133936072602491412 73724587006606315588174881520920962829254091715364 36789259036001133053054882046652138414695194151160 94330572703657595919530921861173819326117931051185 48074462379962749567351885752724891227938183011949 12983367336244065664308602139494639522473719070217 98609437027705392171762931767523846748184676694051 32000568127145263560827785771342757789609173637178 72146844090122495343014654958537105079227968925892 35420199561121290219608640344181598136297747713099 60518707211349999998372978049951059731732816096318 59502445945534690830264252230825334468503526193118 81710100031378387528865875332083814206171776691473 03598253490428755468731159562863882353787593751957 78185778053217122680661300192787661119590921642019 89380952572010654858632788659361533818279682303019 52035301852968995773622599413891249721775283479131 51557485724245415069595082953311686172785588907509 83817546374649393192550604009277016711390098488240 12858361603563707660104710181942955596198946767837 44944825537977472684710404753464620804668425906949 12933136770289891521047521620569660240580381501935 11253382430035587640247496473263914199272604269922 79678235478163600934172164121992458631503028618297 45557067498385054945885869269956909272107975093029 55321165344987202755960236480665499119881834797753 56636980742654252786255181841757467289097777279380 00816470600161452491921732172147723501414419735685 48161361157352552133475741849468438523323907394143 33454776241686251898356948556209921922218427255025 42568876717904946016534668049886272327917860857843 83827967976681454100953883786360950680064225125205 11739298489608412848862694560424196528502221066118 63067442786220391949450471237137869609563643719172 87467764657573962413890865832645995813390478027590 09946576407895126946839835259570982582262052248940 77267194782684826014769909026401363944374553050682 03496252451749399651431429809190659250937221696461 51570985838741059788595977297549893016175392846813 82686838689427741559918559252459539594310499725246 80845987273644695848653836736222626099124608051243 88439045124413654976278079771569143599770012961608 94416948685558484063534220722258284886481584560285 06016842739452267467678895252138522549954666727823 98645659611635488623057745649803559363456817432411 25150760694794510965960940252288797108931456691368 67228748940560101503308617928680920874760917824938 58900971490967598526136554978189312978482168299894 87226588048575640142704775551323796414515237462343 64542858444795265867821051141354735739523113427166 10213596953623144295248493718711014576540359027993 44037420073105785390621983874478084784896833214457 13868751943506430218453191048481005370614680674919 27819119793995206141966342875444064374512371819217 99983910159195618146751426912397489409071864942319 61567945208095146550225231603881930142093762137855 95663893778708303906979207734672218256259966150142 15030680384477345492026054146659252014974428507325 18666002132434088190710486331734649651453905796268 56100550810665879699816357473638405257145910289706 41401109712062804390397595156771577004203378699360 07230558763176359421873125147120532928191826186125 86732157919841484882916447060957527069572209175671 16722910981690915280173506712748583222871835209353 96572512108357915136988209144421006751033467110314 12671113699086585163983150197016515116851714376576 18351556508849099898599823873455283316355076479185 35893226185489632132933089857064204675259070915481 41654985946163718027098199430992448895757128289059 23233260972997120844335732654893823911932597463667 30583604142813883032038249037589852437441702913276 56180937734440307074692112019130203303801976211011 00449293215160842444859637669838952286847831235526 58213144957685726243344189303968642624341077322697 80280731891544110104468232527162010526522721116603 96
