

The Operational Amplifier (Op-Amp) was developed many years ago for analogue computing. This was in the days when the output information from a calculation was readable with a simple voltmeter. Fortunately for us, the Op-Amp can be misused for a huge variety of functions. In this page I will attempt to show what the Op-Amp is and a few uses of it.

Basically, the Op-Amp is nothing more than a differential amplifier that amplifies the difference between two inputs. One input has a positive effect on the output signal, the other input has a negative effect on the output. The component circuit symbol is:
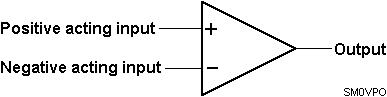
For clarity, the power supply terminals to the amplifier chip are not usually shown, except on detailled circuit diagrams. The Op-Amp requires two power supplies; a positive voltage supply and a negative voltage supply, both with respect to our circuit ground/Earth/chassis connection.
The theoretically perfect Op-Amp has an infinite voltage gain, an infinite bandwidth and infinite input impedances. In this way it just senses an input voltage level without actually interfering with that voltage in any way. The perfect Op-Amp also has a zero-Ohm output impedance. It may therefore be used to drive heavy (in electronic terms) circuits.


Power = Volts X Amperes. So to get an AF power amplifier we must have both volts and current. We have already seen how to build a voltage amplifier, now let us give it a little current capability. We can do this by simply adding a pair of power transistors, one to give positive current, the other to give negative current.
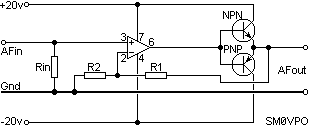
It is quite simple and this particular amplifier will deliver over 20-watts RMS (40-watts Music Power) into a 6-Ohm speaker. It will sound like crap, but at least the power is there (great for RAP music!). Notice how R1 has been moved. In this way the distortion generated by the power transistors will be fed back to generate an "anti-distortion" signal at the output of the Op-Amp. If the voltage gain of the amplifier is set quite low, for example X10 maximum, then the sound of this circuits is quite acceptable. But if you put your head inside the speaker, or increase the gain, then you will hear a very unpleasant distortion at low volume levels. This distortion is called "crossover distortion" and is caused by the transistors not conducting until the signal level has exceeded 0.7vDC. It looks like this on an oscilloscope:
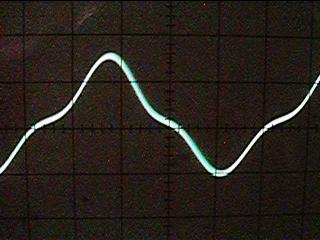
The cure, of course, is to make the transistors conduct a little current when they are idle. The simplest form of conduction bias would be to add resistors and diodes.
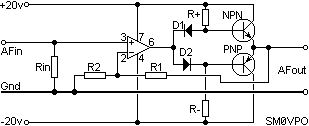
The resistor R+ and D1 provide a bit of current into the base of the NPN transistor. D1 ensures that the DC voltage is the output of the Op-Amp plus 0.7v. R- and D2 do the same at the opposite side for the PNP transistor.

Let us go back to our basic Op-Amp AF amplifier for a few moments, both the circuit and all the internal "gubbins":
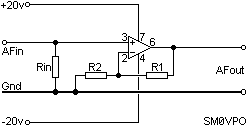 and
and 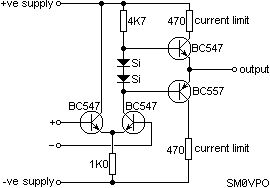
Remember that the Op-Amp may operate from as little as 5v and as high as 40 volts. This gives rise to some form of design conflicts, at least with the cheaper Op-Amp chips. At low signal levels they can distort; crossover distortion generated within the chip. If you want an output signal of, say, +/-10v then there may be no problem at all, but a small high-gain pre-amplifier with an output in the region of 0.1v RMS could suffer terrible crossover distortion. The "cure" for this is to either reduce the gain and/or add a bit of bias current to the output stage.
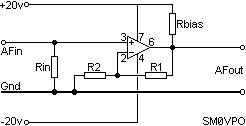
I have now added Rbias which makes one of the output transistors (BC557) conduct permanently. This effectively converts the output stage to a single transistor Class-A amplifer, the other (NPN) transistor never being used.
If you do not wish to muck about with transistors in conjunction with an Op-Amp then choose a "Power Op-Amp" such as the LM2020 which already has the power transistors built-in. This Op-Amp will provide 20 watts of audio. You can even use it to drive motors and lamps. This amplifier must be mounted on a heatsink.

Now you know what an Op-Amp is all about and how it can be used to make amplifiers, let us consider the limitations of frequency response. I have already introduced the concept of "Unity Gain/Bandwidth" (UGB). So let us explore this a little more.
Imagine for one moment that an Op-Amp had a Unity Gain/Bandwidth of 1000000Hz and we used resistors to set the amplifier voltage gain to 190 and then 20. What would the actual frequency response be? This graph shows you exactly what will happen.
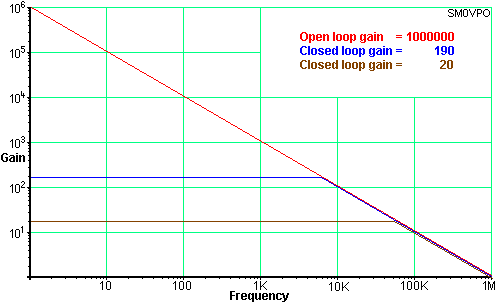
With a voltage gain of 190 set, the amplifier will have a gain of 190, but ONLY up to that frequency where the open-loop gain of the Op-Amp reduces to 190. That point would occur at about 6KHz. Not very good for Hi-Fi reproduction! But if we were to reduce the voltage gain to just 20 then the frequency response would extend to 50KHz. If we needed an amplifier to have a gain of 190 then we would be far better off to have two cascaded amplifier; each with a voltage gain of just 14. The total gain would then be a little over 190 and the frequency response would be DC to over 70KHz.
But is UGB the end of the limitations story? No! Operational amplifiers have another property called "Slew Rate". This means that if the input waveform were to be a square-wave then the output would not change instantaneously. It would take a finite time for the output to change state.
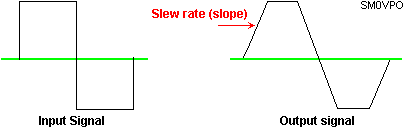
If this slope were shallower than a part of our signal then the signal waveform will distort. If the same waveform were reduced in amplitude then the signal slope would also reduce. This means that the Op-Amp's "slew rate" would affect high-level signals more than low-level signals. Consider the following two output sine-waves with respect to the slew-rate (shown in RED).
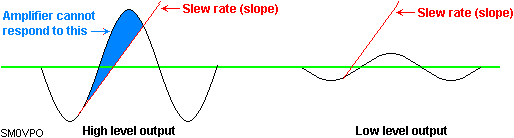
In the first waveform, the signal amplitude is high, so the slope is steep; steeper than the slew rate of the Op-Amp can follow. The waveform will therefore become distorted. The second waveform is of exactly the same frequency, but the signal amplitude is low. The slope of the waveform is therefore less steep than the slew rate of the Op-Amp, so the waveform will be undistorted.
In reality, the Slew rate characteristic of an Op-Amp will only affect signals of a very high frequency, or waveforms having a very steep rise and fall time, for example, square and sawtooth waveforms. For general audio work up to about 30KHz you can normally forget about this effect. The slew rate of an Op-Amp may complicate matters if you try to drive fast logic circuits, such as the 5400 and 7400 series. If you need to drive TTL circuits from Op-Amps then try to choose a logic gate that has a "Schmitt" input function. CMOS gates tend to be a bit more forgiving so you can usually get away with driving them directly from Op-Amps.

The high input impedance of the Op-Amp makes it especially usefull in filter design. Simple RC filters are good, but in order to take an output signal from them you need to load the filter. It is the load that "cocks up" everything. Your load circuit may be resistive, that will affect the responses of the filter. If your load is capacitive or inductive then you have little chance of predicting the outcome with any form of accuracy. So, let us consider the basic Low-Pass filter:
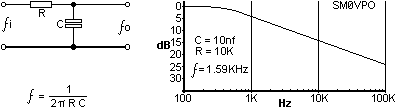
At the frequency of calculation, the output signal will have fallen by 50% of the voltage, or -6dB if you prefer decibels. If you double the frequency then it will have fallen by another 50% (now 25%). Another usefull reference point is the output signal falls by a further 90% every frequency decade. To all intents and purposes, the loss of the filter is zero at F/2. The filter has no gain, in fact, any load at all will cause it to have a loss at all frequencies. This is what we are going to cure first.

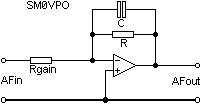
The Op-Amp has simply become a high-impedance buffer stage and has also given the filter a little gain by virtue of (R1+R2)/R2, or R/Rgain in the more conventional circuit. The output impedance is almost zero ohms.
The Op-Amp really "earns it's corn" when you want a little more that 6dB/octave (20dB/decade) rolloff. You could simply cascade two single-pole filters, but inacuracies can enter when one filter is a load for the next. This filter is a 2-pole filter having a rolloff of 12dB/octave (40dB/decade), which in real terms is 25% of the original signal level:
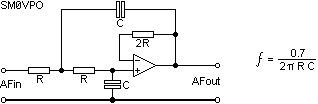
Notice that the turnover formula has changed a little. The 6dB point has now become a 12dB point; the new 6dB point is somewhat lower in frequency, so the 1 in the top line of the formula has become 0.7071 instead. This filter gives a unity gain up to the point it begins to "turnover" - about 0.5/(2 pi R C)

The active high-pass filter is almost the same as the low-pass, but the C and R are exchanged in the circuit to give the opposite response curve. First, the basic high-pass circuit element.
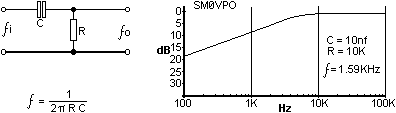
Again, the turnover frequency for the single-pole filter is 1/(2PiCR) and now we shall buffer it with the Op-Amp.
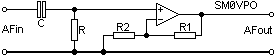
The basic response is still 6dB per octave (20dB per decade) which may not be too usefull for general work. To all intents and purposes, the response is flat from 2/(2PiRC) upwards. Adding an extra RC circuit to make a 2-pole filter will increase the rolloff slope to 12dB per octave.
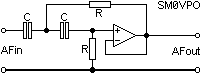
The The losses at 1/(2PiCR) have now increased from -6dB to -12dB so the rolloff point is now 1.41/(2PiRC). I must state here that this only applies for a unity voltage gain (1). To get other voltage gains complicates the formula and they can become quite complex.

This is easy. Use a Low-Pass AND a High-Pass in cascade.

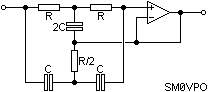
The notch frequency is 1/(2PiRC). The "Gyrator" circuit uses two Op-Amps in a novel circuit where one amplifier inverts the effects of a capacitor which then behaves as an inductor. But I think this has now gone beyond the scope of an article on Op-Amps. But here is the circuit, anyway.
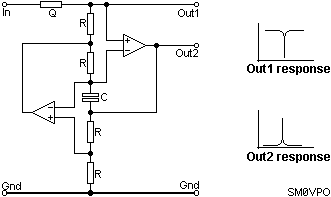
This is one of the circuits that remains firmly planted in my memory, but the brain-failure has extended to the formulas - Sorry! The rough order-of-magnitude is that R is 10K and C is 10nf for somewhere in the middle of the AF band, probably about 1.5KHz. This would imply that 1/(2PiRC) would be the formula, but don't quote me on that. The resistor Q would be about 100K for a bandwidth in the region of about 10Hz or so. Gain is 1 although the output impedance from Out1 is quite high, so an Op-Amp buffer would be needed here.

This is about all I wish to write on this subject. If you are interested in further reading then I suggest you take a trip to your local library. There are several educational Op-Amp books that you may find of interest:
The ARRL Handbook For Radio Amateurs is rather good and easy to understand, but it is a little rudimentary. Assuming you know nothing, you assimilate all the Op-Amp section in one "sitting" on the toilet.
Electronic Circuits (Discrete and integrated) Donald L. Schilling & Charles Belove published by McGraw-Hill International is a real goldmine but tends to be a little "heavy" when it comes to mathematics - I keep my copy in the toilet so I am never short of reading material.
The IC OP-AMP Cookbook" is published by Sams & simply OP-AMPS published by Newnes press are both well worth reading. They contain a lot of useful information for all levels of knowledge. If you seriously wish to learn more, or have an Op-Amp reference data handy, then these are the books for you.
If you want an on-line resource for active filters then you could visit http://www.electronics-tutorials.com/filters/active-bandpass-filters.htm or http://www.filter-solutions.com/active.html where you will find loads of information, although a lot of it is designed to sell filter design software.

Best regards from Harry Lythall - SM0VPO, Lunda, Sweden
Return to INFO page