

At the time of writing this I am patiently waiting for some fine weather so that I can finish my antenna project (it's early January in Sweden with snow), so I am currently winding a transformer for an old project using valves (tubes). I need three different winding objects, the power transformer, smoothing choke, and the speaker transformer. All three have different techniques, since some of them also have a standing DC that could saturate the core. The smoothing choke also needs a specific large inductance.
In this article I will cover all three different types of wound transofrmers, but only those using laminated cores. I will not touch ferrites.

I already have a DIY Transformers project page, but that page is for modifying an existing transformer for a new application and re-using the 230V winding. In this article I will do everything from scratch - all new coils and with (simplified) calculations.
If you google the web you will see 100's of different sites all claiming to give you deep technical knowledge and crunching down those formulas for iron-cored transformers. The formulas look quite daunting, but 99% of all the transformer materials the hobbyist can get hold of are all of the same the same category, which simplifiers the calculations. The number-crunching means one variable multiplied by a constant. That is not so difficult.
I have been re-winding transformers for a number of years, since about 1965. Back in the 1960's my father refused to allow me to have access to the mains 230V AC. He said it was too dangerous for a schoolboy. He DID allow me have a 12V transformer in a sealed box, so that was my opening. My first means of driving a valve was a home-wound transformer 12V AC input to 6.3V AC + 200+200V AC (I knew 200V AC rectified is about 280V DC). So I took apart a 230V to 24V transformer for the wire and I counted the number of turns, then divided it by 24. The result was something like 5, which equals 5 turns per Volt. I didn't know anything about calculating turns per volt, or the power rating of a transformer. My science teacher (Mr. "Test-Tube" Kent) at school could not answer my questions, either.
I thumb-reckoned it was about core area X 30 Watts. That is wrong, but luckily it is close enough for the 20 to 60 Watt area, and I used the home-made formula for about 5 years, until I had Radio Engineers training as an apprentice in the RAF. They didn't teach me the coil calculation formlas either, but they did have a wonderful technical reference library, at RAF Locking, where I would spend many hours. Since those days I have gained a lot of experience, and I have wound transformers for home-made power units, high-current welding, DC-AC power inverters and even re-wound a transformer for an old FT-101ZD, including the inverter coils on it.
This is how I calculate my transformers today:

If you have old transformers with iron cores, then they are almost certainly built to a low price. The more expensive transformers can have processed-steel with a flux density of 12 to 15 kilogauss. Your everyday "el-cheap-o" transformer, as used in battery eliminators, AC-AC voltage converters, etc, will have a flux density more like 10 kilogauss and a rather low permeability value. If you use better cores, then you may need fewer turns per volt, or can have a higher power, but these formulas still work. As my mother used to say, "Expect the worst and you will never be dissapointed".
If you took raw, un-processed iron to make solid cores, then your input winding would draw so much current to heat the core. In effect the core is a big short-circuit winding. The solution is to stack many thin iron laminates, and insulate them. Commercial laminates can be varnished, but the majority of the cheap, domestic transformers, use an insulator between each metal laminate. I have seen them insulated with thin paper or varnish, but the majority for the domestic market use chemicals. These can sometimes break down and cause a little heating, or excessive current. So I ALWAYS spray one side of my laminations with a very thin varnish. So one tip is to measure your laminations for calculating, then spray them to get perfect insulation. You should also make your former a little larger because the varnish increases the thickness a little.
If you use a 50Hz transformer formula then it will work well for both 50Hz and 60Hz transformers, but it will be a bit degraded the other way around.

All the formulas I have found in the 70's were based on the inch, and coil data based on the UK's S.W.G.. Much of the stuff on the web today is based on the US's A.W.G.. I will be using square-millimetres, and mm diameter for wire, so you can look it up yourself. I have given a short table that will give approximate values from 0.05mm Diameter to 2mm Diameter.
Square Inches to Square Millimetres to Square Inches:
To convert square-inches to square millimetres, multiply by 645 (approx). To convert square-inches to square centiimetres, multiply by 6.45. To convert square millimetres or centimetres to square inches, then just divide by 645 or 6.45 (approx). That is dead easy. It can be handy to have a calculator ready programmed, especially if you are doing a lot of calculations:Cross-sectional area:
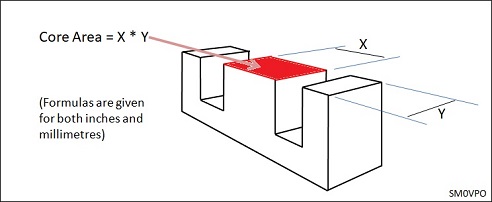
To Calculate cross-Sectional area needed for the centre of a transformer coil:
Formula: mm² = ²√Watts * 116.129323
Formula: inch² = ²√Watts * 0.17921146
Turns per volt:
Now you know the core area, you need to calculate the number of turns per volt.
Formula (50Hz): Turns per volt = 3615.84 / area (mm²)
Formula (60Hz): Turns per volt = 3013.20 / area (mm²)
or ... if you prefer inches:
Formula (50Hz): Turns per volt = 5.58 / area (in²)
Formula (60Hz): Turns per volt = 4.65 / area (in²)

Bare copper wire, 1mm diameter, in air, can easily carry more than 20 Amperes. If it used outside then it may pass 30 amperes on a cold day, unless you live in places like Burkina Faso, Mali, Kiribati, Tuvlu, Senegal or Death Valley in the good old USA. In round figures, at 30 Amperes, a 1mm cross-sectional area copper wire will dissipate about 9 watts per metre with convection cooling (surface area = 3000mm²). As soon as you touch it or cover it, then you get a "hot spot" where there is no convection, and a temperature rise. If the wind is blowing hard then more than 30 Amperes is no problem.
Power cables are covered in plastic, which seriously restricts airflow. That is why you cannot use 1mm diameter cables for more than a few amperes.
There is, however, NO air circulation in a transformer. You have to rely on thermal conduction, and the fact that there are no short-circuits in any winding to cause excessive currents. At the maximum power you want from your transformer, the wire should be capable of handling all the current without any significant temperature rise. For this reason we normally restrict the current to 3 Amperes per square millimeter, which is even less than plastic covered copper.
| Diameter (mm) | SWG | AWG | I-maximum (mA) | Length per 100g reel |
|---|---|---|---|---|
| 0.05 | 47 | 44 | 3.8 | 8200 |
| 0.10 | 41 | 38 | 24 | 1400 |
| 0.15 | 38 | 35 | 54 | 620 |
| 0.20 | 36 | 33 | 75 | 438 |
| 0.25 | 33 | 30 | 147 | 227 |
| 0.30 | 31 | 29 | 212 | 157 |
| 0.35 | 29 | 27 | 288 | 118 |
| 0.40 | 27 | 26 | 377 | 88 |
| 0.45 | 26 | 25 | 476 | 69 |
| 0.50 | 25 | 24 | 585 | 56 |
| 0.60 | 24 | 22 | 849 | 39 |
| 0.70 | 22 | 21 | 1150 | 29 |
| 0.80 | 21 | 20 | 1490 | 21 |
| 0.90 | 20 | 19 | 1850 | 18.5 |
| 1.00 | 19 | 18 | 2350 | 13.5 |
| 1.50 | 17 | 15 | 5250 | 6.3 |
| 2.00 | 14 | 12 | 9350 | 3.4 |

This is probably the most complicated part. The object is to get all the wire you need on the coil winding area. You have to use the required number of turns per volt, otherwide your transformer will get hot and burn. You also have to use the required wire thickness, otherwise it will get hot and burn. Cheap 10 kilogauss laminations leave you with very little space on the coil former, so you have to get the balance just right. If you get it right then you should be able to get your windings within about 80% of the available space budget.
If you are not to worried about regulation (output voltage sagging on load), or running a transformer at maximum power, then you CAN use more turns per volt, or use a core that is larger than needed and use a thicker wire.
Primary Winding
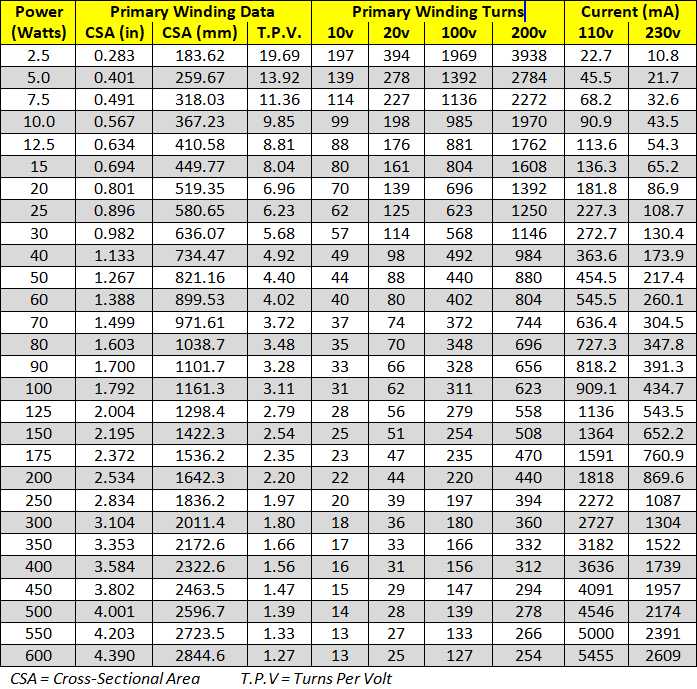
Think about it - a transformer input winding (primary) is the winding that propogates ALL the energy you want to get out of the other windings. The primary winding should therefore occupy 50% of the area budget for ALL the coils. The primary winding should be so dimensioned that it can carry the full primary current. For example, you are to wind a 50-Watt transformer for 250 Volts. The current in the primary will be 50W / 250V = 200mA. From table 1 you can see that you need to make the winding with a minumum of 0.3mm Diameter wire (212mA). For me this is a little close for comfort, so I normally increase the wire size to almost fill the available area. For example, 240V * 5 turns/volt = 1200 turns. Using 0.3mm diameter wire will use 108mm². My budget is 266mm², more than twice this. If I increase the wire diameter to 0.4mm then it will use 192mm² of the 266mm² budget. 0.4mm diameter will also take up to 377mA. This will also reduce the total resistance of the wire and give you better voltage regulation.
My "all-singing" and "all-dancing" transformer primary winding connections in later years has become one winding with taps at 10 - 0 - 100 - 200 - 220 - 240 volts. So with only six connections I can chose an input voltage of 100, 110, 120, 200, 210, 220, 230, 240 and 250 Volts. I can also "rob" a few volts off the primary to feed, for example, fans or indicator lamps. I also have 10V to 40V AC available, in 10 volt steps.
Secondary #1 Winding
To continue with the 50W transformer example, my secondary is 250V - 0 - 250V at 40 Watts. That is to say 500V AV at 80mA. I need to use 0.25mm diameter wire. This secondary winding occupies 40% of the total winding space available: 212mm².
Secondary #2 Winding
The last winding I want is 6.3V AC at 1.5 Amperes (10 Watts). For this will need 0.8mm Diameter wire. This winding should occupy 10% of the available winding space: 52mm².

Transformer laminations are normally punched out of iron sheet in such a way that there is no waste. The geometry is such that the centre-core is usually about twice the thickess as the upper and lower cores. The winding area is usually about 50% of the centre core thickness.
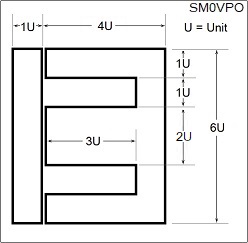
The 4U length of the winding can vary from one manuafacturer to another, as can the number of laminations (core thickness), usually about 30 or so. As regards the number of E's and I's that make up the core, there is absolutely no reason why you cannot "butcher" identical old transformers and put them together, use more laminations, to get a higher powered transformer. If you double the area then you get 4X the power handling (square-law function). 24V AC Christmas-lamps nearly always have exactly the same size laminations. They are perfect for rewinding and making them custom sized.
So my 50 Watt transformer example has a winding area of 48mm long by 15mm deep. My former is 1mm thick, and my 5 spacers are 2mm thick, giving me a winding area of 38 x 14mm = 532 square millimetres; 266 sq-mm for the primary, 106 sq-mm for each of the two 250V secondaries, and 52 sq-mm for the LT winding.
Another point to consider is that if you are to wind a coil with 1mm Diameter wire, then you should be able to wind 12 turns in less than 10 mm². This is probably wishful thinking and practical only if you are a machine. Calculate your wire area as though it is square, and allow a little margin for insurance. Simple rule: winding area / (wire diameter)². Subtract about 25% of the possible turns, unless you are a really neat winder, in which case subtract only 20%. You will always occupy more space than calculated, unless you use a winding machine.
Transformers have a loss, so always wind your secondary windings to give you about 3% more voltage than you want. My primary winding is 240 Volts, at 5 turns per volt = 1200 turns (with 4 tappings). Using 0.4mm diameter wire, there are 0.16 turns per square mm. 1200 * 0.16 = 192 mm² area. Add 10% for insurance = 211 mm². My budget is 266 mm².
My 250V secondary = 258V with the extra 3%. At 5 turns per volt 285 * 5 = 1288 turns. Using 0.25mm² wire I get 90mm², including the 10% safety margin. The budget is 106mm². I need two of these windings. I will have to wind these carefully to save space.
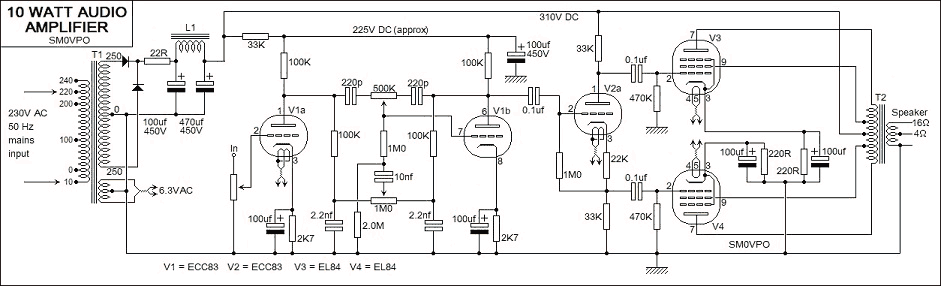
My 6.3v winding is 6.3 * 5 = 31.5 turns. Plus 3% = 32.5 turns. Using 0.8mm diameter wire I have 21mm². My budget is 52mm², but wire as thick as this is not so easy to bend, and it can easily take more space than anticipated. I am happy with such a space budget. Note that I will have two windings of 3.15V, one on top of the other. Look at the circuit diagram.
I stated above that I am having two different winding spaces for my 250-0-250V secondary. Why? If I had one big coil, then several things would happen:
1 - one winding on top of another will have a larger diameter and a different length of wire, with a different resistance.
2 - the wire from the bottom of the coil must pass beside the top of the coil, which means that there will be 500V RMS, or over 700V peak. That can start arcing. Just to be on the safe side, I will divide this secondary into two identical 250V windings, with a high isolation between them.

You can make coil formers from just about anything. 1mm fibre-glass PCB with the copper removed is ideal. On this occasion I am using my 3D printer to make the formers. This also makes the connections more simple as I can add holes to take M3 bolts with solder-tags. Everything is so repeatable. You can fashion formers for small transformers with cardboard and tape, but varnish them afterwards, otherwise then can deform, with time.

My spacers are rather thick (2mm), but with a 50 Watt transformer this is no problem. The core is actually large enough for a 60 Watt transformer, so I have a little budget to play with. 3D printed 2mm spacers means that I can print 6 grooves in every divider so I that can lead out wires without restricting the winding space, and without adding excessive electrical stress on high-voltage windings.
Since I chose 3D printing, I can also quickly print winding spool "end-caps" to clamp the coils, so that I can make a winding tool. The end-caps have a 5.3mm hole in the centre to take a 5mm threaded rod, to which I can fit a winding handle, or grip it in a drill chuck.
If you do not have a 3D printer, then the 1mm thick fibre-glass PCB can look something like this:


If you make a mistake with the windings, then things can happen. For example, if you have two 110V primary windings and connect them in parllel for 110V operation, should one winding be reversed then there will be smoke. If the two windings are not EXACTLY the same number of turns, then there will be heat; the smoke may not be immediate. If any winding has a shorted turn then again the transformer will draw more current. Testing is important.
The easiest way to test a 110V or 220V mains transformer is to connect the primary winding in series with an electric lamp. I still have loads of 15W and 40W tungsten fillamant lamps. A 15-Watt tungsten lamp has a resistance of 3500Ω when it is lit. But when it is cold, the resistance can be more like 250Ω. As it gets hot, so the resistance rises until the lamp gets to it's working temperature. This effect can be used to test your transformers.
Connect the lamp in series with the transformer winding. If the reactance of the transformer winding is very high at 50Hz (60Hz) then the lamp should remain dark. If you have a complete short-circuit, then instead of a loud bang when you switch ON the power, then all that will happen is that the lamp will light. It should glow so weakly that you cannot see it at all. If you have short-circuit turns of wire in your transformer, or if you deliberately short one of the windings, then the lamp will glow.

Incidentally, this technique used to be used extensively. Telephone systems, with 50V DC down the line, had "baretta" lamps used to limit current (and strung together to make the worlds first private Xmas-tree illuminations, by an amorous Boston telephone trying to impress a telephone operator, circa 1904). They even used the in the RX antenna circuit of the FT-101ZD to protect the receiver from an RF overload.
Ok, so you have applied power, nothing has smoked, the lamp is not lit and the transformer has input power. Now all you need do is check the voltages of the windings. The voltages should be about 2% high off-load, but this will fall a little when you try to draw any current. If you have several primary windings then wire them in series and check each terminal to be sure that the windings are in the correct phase. If you have, for example, a 20V winding and a 100V winding, then when series connected you should see 20V, 100V and 120V from the expected winding.
If all is well, then you can remove the series test-lamp and use something to load the secondary windings. Again, lamps are good for this. Today you can get them in 12V, 120V and 230V variants, and with different power ratings. Let the transformer run for an hour or so to check that there is no excessive heat. A correctly designed and built transformer should be no more than slightly warm to the touch.

I don't now about you, but I like to write my data in tables, then store them on folders. Always handy, even if I don't have access to the my homepages, or cannot remember the formulas. So here is a quick-reference guide to winding transformers. Please note that, as stated at the beginning, this table is designed around your ordinary, cheap iron formers, as made in China, Spain and commonly available for Christmas-tree lights, printer/modem power supplies, etc.
One last word of warning before I go on to speaker transformers, re-using transformers is really good if there are already, say, primary or secondary windings that you can re-use. Check the windings before you use them. The transformer core I have worked on in this project started out life as a 250W, 115V to 230V auto-transformer so that you can power equipment designed for other countries. I bought it from a small high-street market shop in Saudi Arabia. It was marked "Made in Spain". The thing burned out after an hour with no load.

On inspection I saw that only about 15% of the winding area was used. Then I found that a magnet would stick to the enamelled wire: it wasn't even copper!! Touching the burned wire felt like touching sand-paper. So if you are to re-use windings or wire, then be very careful. Manufacturers do cut corners to reduce costs, which is why I always spray-paint my laminations. Use new wire whenever you can.

The second type of transformer in my amplifier project will match the output impedance of the output stages to the speaker load impedance. For this type of transformer there are special types of core material. Ordinary iron core laminations for power transformers give some latency with the magnetic fields, which has the effect of reducing the higher frequencies. The formulas are quite involved.
I have found that you CAN use ordinary power transformer laminations, but you have to adjust the formulas a little to account for the frequency range. The formulas for power transformers are intended for 50Hz (60Hz) but for audio work you may be interested in different lower frequencies. For example, for communication you mey only need a lower frequency of 200Hz, but for music you can use 50Hz formulas. In my amplifier I want to have 20Hz as my lowest working frequency, so the formulas I use are:
Cross-sectional area:
To Calculate cross-Sectional area needed for the centre of a transformer coil:
Formula: mm² = ²√Watts * 116.129323
Formula: inch² = ²√Watts * 0.17921146
This is exactly the same as for power transformers. No problem, it works.
To get the number of turns, however, I have to take into account the lowest frequency for my transformer. To do this I use the formula:
Turns per volt:
Now you know the core area, you need to calculate the number of turns per volt.
Formula: Turns per volt = 180792 / Frequency(Hz) * area(mm²)
or ... if you prefer inches:
Formula: Turns per volt = 279 / Frequency(Hz) * area(in²)
|
|
|
Input Voltage:
If you have a single Class-A amplifier, then the signal input voltage at the collector of the transistor, or the anode of the valve (tube) is = (Vcc/2) * ²√2. So with my audio power amplifier I have 310 Volts supply. Divided by 2 = 150V. Multiplied by ²√2 (1.4142135) = 106V RMS. I will call it just 100V RMS because no amplifying device will use the full supply voltage as the output signal. Turns per volt from the above area/frequency calculation, multiplied by 100V gives me the total number of turns I need to wind on my speaker transformer.
Anode Impedance to Speaker Impedance
My two push-pull valves will deliver a total signal voltage of 200 Volts RMS (100V per valve) and the power level is 12.6 Watts. Impedance is E²/W = 200V * 200V / 12.6W = 40,000 / 12.6 = 3,174Ω. My speaker impedance is 16Ω, so my impedance ratio is (3,174/16):1 = 198:1. The turns ratio = ²√Impedance-ratio = ²√198:1 = 14.1:1.
Going back to the transformer core, I have a 12-Watt transformer from an old 12V 1A power unit. The core area is 420mm². From the above calculators I see that 420mm² core area, at 20Hz gives me 21.522 turns per volt. 21.522 * 200-Volts = 4305 turns for the primary winding. 4305 turns, divided by 14.1 = 305 turns for the speaker secondary winding, tapped at 152 turns for the 4Ω winding. The primary must take a current of 50mA, so refering to the table, I need 0.15mm diameter wire for the primary, which will occupy only 97mm² of space on the core. The secondary winding needs 0.5mm diameter, or 175mm² of core winding area. Since the audio is never 100% continuously, the transformer will only be passing power for very short durations, so the wire size can be reduced, if necessary. My core winding available area is well over 350mm² so there is more than enough space for the coils.
The only problem is that standing DC current drawn by the valves. 50mA is quite a lot. It will give the core a standing magnetic bias, so I have to somehow break the magnetic loop a little. In practice I can do this by inserting all the E laminations from one side of the coil, and all the I laminations from the other, BUT they are seperated by 0.1mm of photocopy paper. If the standing current was only 5 or 10mA then the break due to butting the E's directly to the I's would be sufficient.
I like cheating. I really love modifying components to do other jobs. All the above playing around will in fact give me a transformer that will convert 250V AC to 48V AC. This means that an "off-the-shelf" 230V to 24-0-24V will do the same job. The lower frequency response will be about 35Hz. All you need to do is to strip it down and re-assemble with all the E's and I's in the same direction and use the paper magnetic-break. If the amplifier is used for pop-music then no-one will ever notice the difference. If you want to use the amplifier for a bass guitar then you will need to make your own.
The finished speaker transformer must be varnished and so secured that it cannot vibrate. That completes my speaker transformer.

This is also very easy to calculate. All you need coil on an iron-laminate former. The smoothing capacitors in the circuit (100uf and 450uf) have impedances of 15Ω and 3.5Ω respectively (at 100Hz, the ripple from a full-wave rectifier). The AC impedance of the coil only needs to be about 50Ω to give a 6dB reduction in ripple. 300mH will do this. But if I have 3 Henries then the impedance to 100Hz will rise to 3,140 Ω. This will give me a ripple rejection of much better than 40dBV, which is a lot more than I really need; just a mere fraction of 1%.
Once more, an "off-the-shelf" transformer will also do the same job, if you strip it down and re-assemble with all the E's and I's in the same direction and use the paper magnetic-break. For smoothing chokes in power supplies, the DC component is really important, and the DC resistance of the wire can drop a lot of voltage if the wire is too thin. If the core is allowed to saturate then the inductance falls rapidly. Although there are calculation you can do, simply using a double paper insulator (0.2mm) between the E's and the I's is allthat is needed in practice.

Let us assume we have a load of iron laminations to make a choke, and we need 5 Henries. If you have the data for the incremental AC permeability data (µ) for the laminations, then use this. If you have no data then assuming µ = 1000 is a fairly safe value to use. You also need to know the core area and the core magnetic path length.
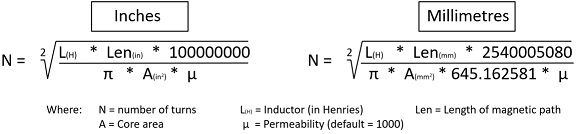
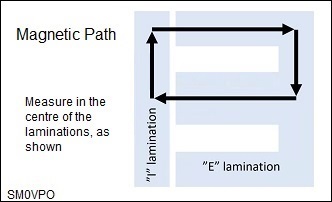
|
|


Well I hope that you have learned something useful with this information. Very best regards from Harry - SM0VPO
Return to INDEX page