

In many of my articles I have stated that one should always use a filter in the output of a transmitter. The type of filter can be different, depending on the transmitter. There is no such thing as a perfect transmitter and all transmitter are "dirty" to some degree. The choice of filter can also be affected by the transmitter frequency in the radio spectrum.
In this article I will discuss a standard Low-Pass filter, a High-Pass filter and an Elliptic filter to get a really sharp cutoff, if required. But I will keep it really simple and not go into any great depth. I will just give a minimum requirement and a simple solution.
I have given the eponymic names of the filter configurations, so that you can google them and learn more about their properties. So let us continue with a basic filter. Purely hypothetically, assume we own a very small island with a large population. Let us call it "Mingingo island".

Consider a hypothetical 31m (9.4MHz to 9.9MHz) AM transmitter operating at 9.899MHz, pushing out just 1-Watt. All the fishermen can listen to the weather broadcast on their little Sony World Radios. The spectrum analyser may show a frequency spectrum something like this:
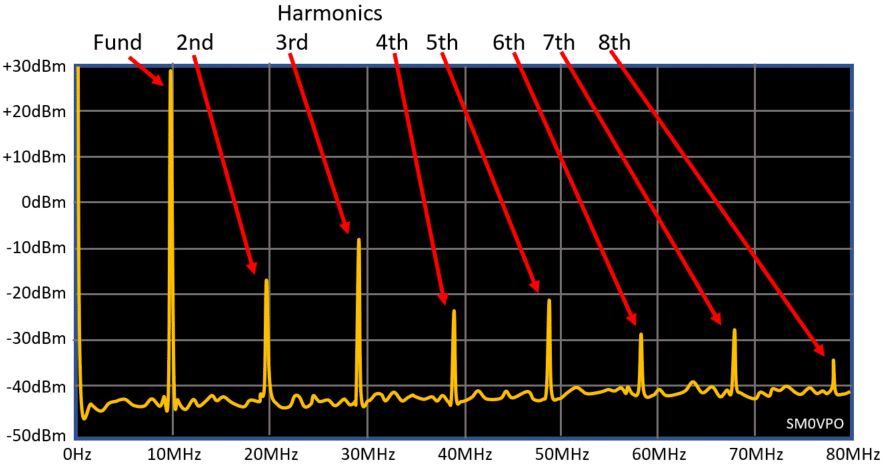
As you can see there are several points of interest:

This transmitter needs an output filter. The odd harmonics (3rd, 5th, 7th, etc) are usually stronger than the even harmonics because odd harmonics are created by clipping, or when an output stage is approaching it amplitude limits. A good figure to aim for is -90dBm (7.07µV), so we should really have about 80dB of rejection at the 3rd harmonic (worst case). Resonant antennas offer some form of filtering but you can expect only 20dB of rejection, because resonant dipole antennas also work on the 3rd and odd harmonics. So our minimum requirement for this transmitter is a low-pass filter with a cut-off "knee" at around 11MHz. The filter will start to attenuate signals at about 10MHz. A simple 7-pole Low-Pass filter will do this.
If your transmitter was operating in the VHF FM broadcast band then you have the added complication of the VHF aircraft band, which is VERY close to the FM band. If the transmitter is not well designed then there could be spurious output very close to the operating frequency, especially if the final stage device is run anywhere near it's recommended operating limits. In this event you will need a really sharp cut-off at 108MHz, and a simple Low-Pass filter is not sufficient. You should really look at the elliptical high-pass filter, where additional resonances are added to give a couple of "notches" of additional attenuation immediately after the cut-off frequency. You should also accept a small loss of 1dB or so at the upper frequency of your transmitter. So let us look at different band-pass filter responses:
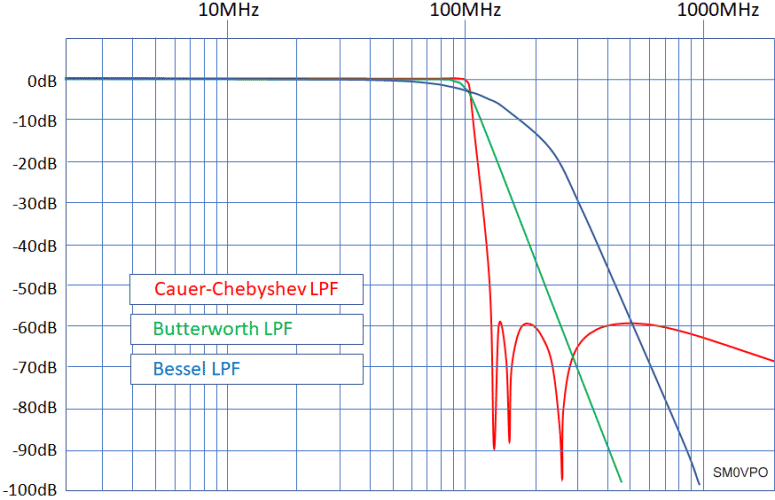
As you can see, the Bessel Low-Pass filter is nothing to have and has high losses just before the cutoff. The basic LPF (eg. Butterworth) is great for the usual harmonic filters as used in HF transmitting equipment. VHF FM transmitters, however, need something better due to the frequency proximity to the aircraft band. In this event you should use an Elliptic filter (eg. Cauer-Chebyshev). In this article I will consider only these two filter types, but I will give the component values for 7-pole filters. A 7-pole filter means that there are 7 reactive components that affect the frequency.
Note that I have not given the actual component values in loads of tables. I have specified specified the reactance of the components, in Ohms (Ω). This means that you can easily calculate the component value for any frequency you like. You will find on-line calculators for inductors and capacitors on my Radio Calculators page (opens in a new tab). I have added an on-line calculator for each of these three filter options.

A basic low-pass filter is symetrical and consists of four capacitors and three inductors. This particular filter design has a reasonable flat response and low loss, up to the cut-off "knee". Expect in the region of 6dB for every element in the filter at twice the cut-off frequency. This filter has 7 poles, so expect a reduction of (6dB X 7-poles) 42dB at the 2nd harmonic, and 66dB at the 3rd harmonic. The 5th harmonic could be 100dB, but this depends a lot on the construction technique.
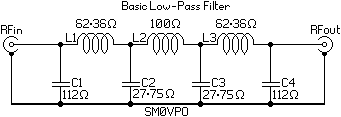

In some applications, for example, where you are converting up to a higher frequency, you may need to use a High-Pass filter to stop the lower frequencies from being passed to the next stage. The same filter as above works. All you need do is change the inductors for capacitors, and change the capacitors for inductors. Could not be easier.
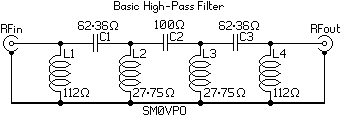

In applications where you want some serious reduction at the point of cutoff, the basic 7-pole LPF filter is not suitable. If you are building a VHF FM transmitter for 88MHz to 108MHz, then you can get spurious outputs close to the fundamental frequency. You need a really sharp cut-off, and that cutoff should be as close to 108MHz as possible, as discussed at the beginning of this page. The Elliptic LPF is a modification to adds series resonances just above the maximum frequency. These additional resonances are done by adding C2, C4 and C6.
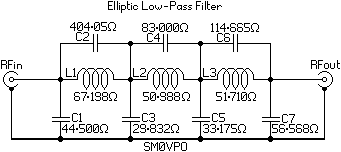
This will give a theoretical 20dB reduction of spurious output at 118.8MHz, which is only 10MHz above the cut-off frequency. The measured response of my prototype was about -60dB at 135MHz. The filter I built followed the graph very closely, but the capacitor and coil values are extremely critical. If you have a Vector Network Analyser (VNA) then you can adjust the geometry of the three coils a little to get a perfect response.

If you do calculate the values then you may find yourself looking some WeIrDe capacitor values. For example, 49.31pf. You could use trimmer capacitors and make adjustments, but that will be a mammoth task to get it right. In my recent projects I have used PCB pads for two capacitors in parallel, so that you could use a 4.7pf and a 2.2pf in parallel to get 49.2pf.
"Normal" ceramic capacitors can have a wide tolerance, and change their value with temperature changes. You should always select temperature-stable capacitors, such as NPO. These are usually marked with a black dot on the top of the components and have a stability of typically better than <0.4% between −40°C to 120°C. Mica capacitors are still available in 1% tolerances, and you can get then in 2220 SMT packaging. A lot depends on the accuracy you want and the type of filter you need.

In this article I have given you three practical filter designs that can be scaled to any frequency you want, from a few tens of KHz to about 400MHz. If you google the Low-Pass Filter then you will find 100's of designs, most of which are based on these two configurations I have given you.
With this information you should be able to clean up your transmitters and practically eliminate interference to other services. There is absolutely no valid reason for using a "dirty" transmitter.

I hope that this project has given you some "food for thought". You can always e-mail me at harry.lythall@[my domain].com. You can even use oeieio@hotmail.com or hotmail@sm0vpo.com as they are both valid e-mail accounts for me 😉 although I would prefer that you visit my messageboard if you have any questions about this or any other project. I always look forward to receiving feedback, positive or negative 🙂

Very best regards from Harry - SM0VPO
Return to INFO page